what is the speed of a spacecraft that makes the trip in 5.5 min according to its on-board clocks?

5.4: Time Dilation

1. Final updated

2. Relieve as PDF

Page ID

4515

Learning Objectives

By the end of this section, y'all will be able to:

• Explain how time intervals tin be measured differently in different reference frames.
• Describe how to distinguish a proper fourth dimension interval from a dilated time interval.
• Describe the significance of the muon experiment.
• Explicate why the twin paradox is non a contradiction.
• Calculate time dilation given the speed of an object in a given frame.

The analysis of simultaneity shows that Einstein's postulates imply an of import effect: Time intervals have unlike values when measured in dissimilar inertial frames. Suppose, for example, an astronaut measures the time it takes for a pulse of light to travel a distance perpendicular to the management of his ship's motion (relative to an earthbound observer), bounce off a mirror, and return (Figure \(\PageIndex{1a}\)). How does the elapsed fourth dimension that the astronaut measures in the spacecraft compare with the elapsed time that an earthbound observer measures by observing what is happening in the spacecraft?

Examining this question leads to a profound upshot. The elapsed time for a process depends on which observer is measuring it. In this case, the fourth dimension measured by the astronaut (inside the spaceship where the astronaut is at rest) is smaller than the time measured by the earthbound observer (to whom the astronaut is moving). The fourth dimension elapsed for the same procedure is unlike for the observers, considering the distance the light pulse travels in the astronaut'south frame is smaller than in the earthbound frame, every bit seen in Figure \(\PageIndex{1b}\). Light travels at the aforementioned speed in each frame, so it takes more than time to travel the greater distance in the earthbound frame.

Figure \(\PageIndex{1}\): (a) An astronaut measures the time \(\Delta \tau\) for lite to travel distance 2D in the astronaut's frame. (b) A NASA scientist on Earth sees the calorie-free follow the longer path 2s and take a longer time \(\Delta t\). (c) These triangles are used to find the relationship between the two distances D and s.

Definition: Fourth dimension Dilation

Fourth dimension dilation is the lengthening of the time interval between 2 events for an observer in an inertial frame that is moving with respect to the residuum frame of the events (in which the events occur at the same location).

To quantitatively compare the time measurements in the ii inertial frames, we can relate the distances in Figure \(\PageIndex{1b}\) to each other, so express each altitude in terms of the time of travel (respectively either \(\Delta t\) or \(\Delta \tau\)) of the pulse in the corresponding reference frame. The resulting equation tin so exist solved for \(\Delta t\) in terms of \(\Delta \tau\).

The lengths \(D\) and \(50\) in Figure \(\PageIndex{1c}\) are the sides of a right triangle with hypotenuse \(southward\). From the Pythagorean theorem,

\[s^2 = D^ii + 50^two. \nonumber\]

The lengths \(2s\) and \(2L\) are, respectively, the distances that the pulse of lite and the spacecraft travel in time \(\Delta t\) in the earthbound observer's frame. The length \(D\) is the distance that the light pulse travels in time \(\Delta \tau\) in the astronaut's frame. This gives us three equations:

\[\begin{marshal*} 2s &= c\Delta t \\[4pt] 2L &= v\Delta t; \\[4pt] 2nd &= c\Delta \tau. \end{align*}\]

Note that we used Einstein'south second postulate by taking the speed of calorie-free to be c in both inertial frames. We substitute these results into the previous expression from the Pythagorean theorem:

\[ \begin{align*} s^ii &= D^2 + L^2 \\[4pt] \left(c\dfrac{\Delta t}{2}\right)^two &= \left(c\dfrac{\Delta \tau}{2}\correct)^2 + \left(5\dfrac{\Delta t}{2}\right)^2 \end{marshal*}\]

And then we rearrange to obtain

\[(c\Delta t)^2 - (v\Delta t)^2 = (c\Delta \tau)^ii. \nonumber\]

Finally, solving for \(\Delta t\) in terms of \(\Delta \tau\) gives u.s.

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - (5/c)^2}}. \nonumber\]

This is equivalent to

\[\Delta t = \gamma \Delta \tau, \label{timedilation}\]

where \(\gamma\) is the relativistic factor (frequently called the Lorentz gene) given by

\[\gamma = \dfrac{1}{\sqrt{ane - \dfrac{v^2}{c^2}}}\]

and \(v\) and \(c\) are the speeds of the moving observer and light, respectively.

Note the disproportion betwixt the two measurements. Only one of them is a measurement of the time interval betwixt two events—the emission and inflow of the lite pulse—at the same position. Information technology is a measurement of the fourth dimension interval in the remainder frame of a single clock. The measurement in the earthbound frame involves comparing the fourth dimension interval between two events that occur at different locations. The time interval between events that occur at a single location has a separate name to distinguish it from the time measured by the earthbound observer, and nosotros employ the split symbol \(\Delta \tau\) to refer to information technology throughout this chapter.

Definition: Proper Time

The proper fourth dimension interval \(\Delta \tau\) betwixt two events is the time interval measured by an observer for whom both events occur at the aforementioned location.

The equation relating \(\delta t\) and \(\Delta \tau\) is truly remarkable. First, as stated earlier, elapsed time is not the aforementioned for dissimilar observers moving relative to one another, even though both are in inertial frames. A proper fourth dimension interval \(\Delta \tau\) for an observer who, like the astronaut, is moving with the appliance, is smaller than the time interval for other observers. It is the smallest possible measured time betwixt ii events. The earthbound observer sees time intervals inside the moving system every bit dilated (i.eastward., diffuse) relative to how the observer moving relative to Earth sees them within the moving system. Alternatively, according to the earthbound observer, less fourth dimension passes between events within the moving frame. Note that the shortest elapsed time between events is in the inertial frame in which the observer sees the events (e.yard., the emission and arrival of the light point) occur at the same bespeak.

This time effect is real and is not caused by inaccurate clocks or improper measurements. Fourth dimension-interval measurements of the same outcome differ for observers in relative motion. The dilation of time is an intrinsic property of time itself. All clocks moving relative to an observer, including biological clocks, such every bit a person's heartbeat, or aging, are observed to run more than slowly compared with a clock that is stationary relative to the observer.

Note that if the relative velocity is much less than the speed of light (v << c), then \(v^2/c^2\) is extremely pocket-size, and the elapsed times \(\Delta t\) and \(\Delta \tau\) are well-nigh equal. At low velocities, physics based on modern relativity approaches classical physics—everyday experiences involve very small relativistic effects. Notwithstanding, for speeds near the speed of light, \(five^two/c^ii\) is close to i, so \(\sqrt{ane - v^ii/c^ii}\) is very pocket-size and \(\Delta t\) becomes significantly larger than \(\Delta \tau\).

Half-Life of a Muon

There is considerable experimental evidence that the equation \(\Delta t = \gamma \Delta \tau\) is correct. Ane case is institute in cosmic ray particles that continuously rain downward on Earth from deep space. Some collisions of these particles with nuclei in the upper atmosphere consequence in curt-lived particles called muons. The half-life (amount of time for half of a material to decay) of a muon is i.52 μs when it is at rest relative to the observer who measures the half-life. This is the proper time interval \(\Delta \tau\). This brusque time allows very few muons to attain Earth's surface and be detected if Newtonian assumptions about time and infinite were correct. Withal, muons produced by cosmic ray particles have a range of velocities, with some moving near the speed of light. It has been found that the muon's half-life equally measured by an earthbound observer (\(\Delta t\)) varies with velocity exactly equally predicted by the equation \(\Delta t = \gamma \Delta \tau\). The faster the muon moves, the longer it lives. Nosotros on World see the muon last much longer than its half-life predicts within its ain balance frame. As viewed from our frame, the muon decays more slowly than it does when at rest relative to u.s.. A far larger fraction of muons reach the footing as a upshot.

Before we present the commencement example of solving a problem in relativity, nosotros country a strategy you tin use equally a guideline for these calculations.

Problem-SOLVING STRATEGY: RELATIVITY

1. Make a list of what is given or can exist inferred from the problem equally stated (place the knowns). Expect in particular for information on relative velocity v.
2. Identify exactly what needs to be determined in the problem (place the unknowns).
3. Make certain you lot understand the conceptual aspects of the problem before making any calculations (express the answer as an equation). Decide, for example, which observer sees fourth dimension dilated or length contracted before working with the equations or using them to conduct out the calculation. If yous accept thought about who sees what, who is moving with the consequence beingness observed, who sees proper time, then on, you volition find it much easier to determine if your calculation is reasonable.
4. Determine the master type of adding to be done to detect the unknowns identified in a higher place (exercise the adding). You volition find the section summary helpful in determining whether a length contraction, relativistic kinetic energy, or another concept is involved.

Note that y'all should not round off during the adding. As noted in the text, y'all must often perform your calculations to many digits to come across the desired effect. You may circular off at the very finish of the problem solution, but practise non employ a rounded number in a subsequent calculation. Besides, bank check the reply to see if information technology is reasonable: Does information technology make sense? This may be more hard for relativity, which has few everyday examples to provide experience with what is reasonable. Merely yous tin can expect for velocities greater than c or relativistic effects that are in the wrong direction (such as a time contraction where a dilation was expected).

Example \(\PageIndex{1A}\): Time Dilation in a High-Speed Vehicle

The Hypersonic Engineering science Vehicle ii (HTV-2) is an experimental rocket vehicle capable of traveling at 21,000 km/h (5830 m/south). If an electronic clock in the HTV-2 measures a fourth dimension interval of exactly 1-s duration, what would observers on Earth measure the fourth dimension interval to be?

Strategy

Apply the time dilation formula to relate the proper time interval of the signal in HTV-2 to the time interval measured on the footing.

Solution

1. Identify the knowns: \(\Delta \tau = 1 \, due south\); \(5 = 5830m/s.\)
2. Identify the unknown: \(\Delta t\).
3. Express the respond as an equation:

   \[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{i - \dfrac{v^2}{c^2}}}. \nonumber\]

4. Practise the calculation. Use the expression for \(\gamma\) to determine \(\Delta t\) from \(\Delta \tau\):

   \[\brainstorm{align*} \Delta t &= \dfrac{1 \, southward}{\sqrt{1 - \left(\dfrac{5830 \, m/s}{3.00 \times ten^eight m/s}\right)^ii}} \\[4pt] &= one.000000000189 \, s \\[4pt] &= 1 \, s + 1.89 \times 10^{-x}s. \end{align*}\]

Significance

The very loftier speed of the HTV-2 is yet only 10^-five times the speed of light. Relativistic effects for the HTV-2 are negligible for almost all purposes, but are non zilch.

What Speeds are Relativistic?

How fast must a vehicle travel for 1 second of time measured on a passenger'due south lookout man in the vehicle to differ by 1% for an observer measuring it from the ground outside?

Strategy

Use the time dilation formula to find v/c for the given ratio of times.

Solution

1. Place the known:

   \[\dfrac{\Delta \tau}{\Delta t} = \dfrac{1}{ane.01}. \nonumber\]

2. Identify the unknown: v/c.
3. Limited the answer every bit an equation:

   \[ \begin{align*} \Delta t &= \gamma \Delta \tau \\[4pt] &= \dfrac{1}{\sqrt{1 - 5^2/c^two}}\Delta \tau \\[4pt] \dfrac{\Delta \tau}{\Delta t} &= \sqrt{1 - five^2/c^2} \\[4pt] \left(\dfrac{\Delta \tau}{\Delta t}\correct)^ii &= ane - \dfrac{v^2}{c^two} \\[4pt] \dfrac{v}{c} &= \sqrt{1 - (\Delta \tau/\Delta t)^2}. \cease{align*}\]

4. Practise the calculation:

   \[\dfrac{v}{c} = \sqrt{one - (1/i.01)^2} = 0.14. \nonumber\]

Significance

The effect shows that an object must travel at very roughly ten% of the speed of low-cal for its motion to produce pregnant relativistic time dilation effects.

Calculating \(\Delta t\) for a Relativistic Issue

Suppose a catholic ray colliding with a nucleus in Earth's upper atmosphere produces a muon that has a velocity \(5 = 0.950c\). The muon then travels at constant velocity and lives two.xx μs as measured in the muon's frame of reference. (Yous can imagine this as the muon's internal clock.) How long does the muon live equally measured past an earthbound observer (Figure \(\PageIndex{2}\))?

Figure \(\PageIndex{2}\): A muon in World'southward atmosphere lives longer as measured by an earthbound observer than as measured by the muon'due south internal clock.

As nosotros will discuss later, in the muon's reference frame, it travels a shorter distance than measured in World's reference frame.

Strategy

A clock moving with the muon measures the proper fourth dimension of its decay process, and then the time we are given is \(\Delta \tau = ii.xx \mu due south\). The earthbound observer measures \(\Delta t\) as given by the equation \(\Delta t = \gamma \Delta \tau\). Because the velocity is given, we can summate the time in Earth's frame of reference.

Solution

1. Identify the knowns: \(v = 0.950c\); \(\delta \tau = 2.20 \mu s\).
2. Identify the unknown: \(\Delta t\).
3. Express the reply as an equation. Use:

   \[\Delta t = \gamma \Delta \tau. \nonumber\]

   with

   \[\gamma = \dfrac{1}{\sqrt{1 - \dfrac{v^2}{c^2}}}. \nonumber\]

4. Do the adding. Use the expression for \(\gamma\) to determine \(\Delta t\) from \(\Delta \tau\):

   \[\begin{align*} \Delta t &= \gamma \Delta \tau. \\[4pt] &=\dfrac{one}{\sqrt{1 - \dfrac{5^2}{c^2}}}\delta \tau \\[4pt] &=\dfrac{2.twenty \mu south}{\sqrt{i - (0.950)^2}} \\[4pt] &= vii.05 \, \mu s.\end{align*}\]

   Remember to go along actress significant figures until the final answer.

Significance

One implication of this example is that because \(\gamma = 3.xx\) at 95.0% of the speed of light (\(v = 0.950c\)), the relativistic furnishings are pregnant. The two time intervals differ by a factor of 3.xx, when classically they would be the aforementioned. Something moving at 0.950c is said to be highly relativistic.

Example \(\PageIndex{1B}\): Relativistic Television set

A non-flat screen, older-way television display (Figure \(\PageIndex{3}\)) works by accelerating electrons over a short altitude to relativistic speed, then using electromagnetic fields to control where the electron beam strikes a fluorescent layer at the front end of the tube. Suppose the electrons travel at \(6.00 \times 10^7 yard/s\) through a distance of 0.200m0.200m from the offset of the beam to the screen.

1. What is the time of travel of an electron in the balance frame of the television set?
2. What is the electron's time of travel in its ain residual frame?

Figure \(\PageIndex{3}\): The electron beam in a cathode ray tube goggle box brandish.

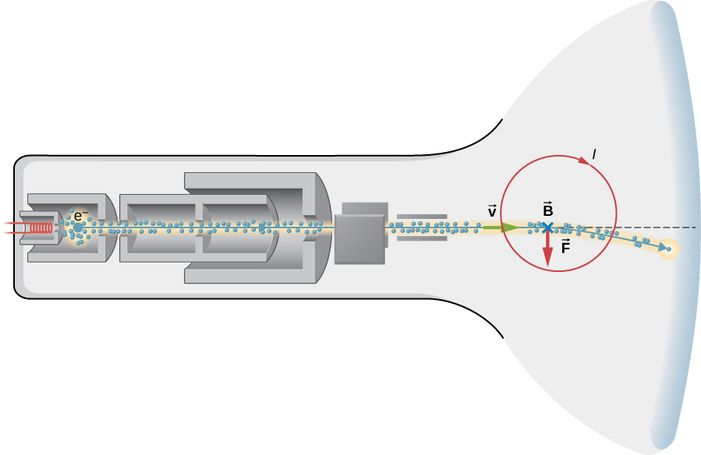
Strategy for (a)

(a) Summate the time from \(vt = d\). Even though the speed is relativistic, the calculation is entirely in one frame of reference, and relativity is therefore not involved.

Solution

1. Identify the knowns:

   \[5 = 6.00 \times 10^7 m/southward \, d = 0.200 \, m. \nonumber\]

2. Identify the unknown: the time of travel \(\Delta t\).
3. Express the reply as an equation:

   \[\Delta t = \dfrac{d}{v}. \nonumber\]

4. Do the adding:

   \[ \begin{marshal*} t &= \dfrac{0.200 \, chiliad}{6.00 \times 10^vii \, chiliad/s} \\[4pt] &= 3.33 \times x^{-ix} \, s. \finish{align*}\]

Significance

The time of travel is extremely short, equally expected. Because the calculation is entirely within a unmarried frame of reference, relativity is not involved, even though the electron speed is close to c.

Strategy for (b)

(b) In the frame of reference of the electron, the vacuum tube is moving and the electron is stationary. The electron-emitting cathode leaves the electron and the forepart of the vacuum tube strikes the electron with the electron at the aforementioned location. Therefore nosotros use the time dilation formula to relate the proper time in the electron rest frame to the fourth dimension in the television receiver frame.

Solution

1. Place the knowns (from part a):

   \[\Delta t = 3.33 \times x^{-nine} \, s; \, v = half dozen.00 \times 10^seven \, thousand/southward; \, d = 0.200 \, m. \nonumber\]

2. Identify the unknown: \(\tau\).
3. Limited the answer equally an equation:

   \[\Delta t = \gamma \Delta \tau = \dfrac{\Delta \tau}{\sqrt{ane - 5^2/c^2}}. \nonumber\]

4. Do the adding:

   \[\begin{align*} \Delta \tau &= (iii.33 \times 10^{-9}s)\sqrt{1 - \left(\dfrac{6.00 \times 10^7 m/s}{three.00 \times x^viii thou/due south}\right)^2} \\[4pt] &= iii.26 \times 10^{-ix}s. \end{marshal*}\]

Significance

The time of travel is shorter in the electron frame of reference. Because the problem requires finding the time interval measured in different reference frames for the same procedure, relativity is involved. If we had tried to calculate the time in the electron rest frame by but dividing the 0.200 thou by the speed, the result would be slightly incorrect considering of the relativistic speed of the electron.

Exercise \(\PageIndex{1}\)

What is \(\gamma\) if \(5 = 0.650c\)?

Reply

\[\gamma = \dfrac{ane}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{1}{\sqrt{1 - \dfrac{(0.650c)}{c^2}}} = one.32 \nonumber\]

The Twin Paradox

An intriguing consequence of fourth dimension dilation is that a space traveler moving at a loftier velocity relative to Earth would age less than the astronaut's earthbound twin. This is often known as the twin paradox. Imagine the astronaut moving at such a velocity that \(\gamma = 30.0\), equally in Figure \(\PageIndex{four}\). A trip that takes two.00 years in her frame would take 60.0 years in the earthbound twin's frame. Suppose the astronaut travels 1.00 year to another star system, briefly explores the expanse, and and so travels ane.00 year back. An astronaut who was forty years old at the kickoff of the trip would be would be 42 when the spaceship returns. Everything on Earth, however, would have aged 60.0 years. The earthbound twin, if still alive, would exist 100 years one-time.

The situation would seem different to the astronaut in Figure \(\PageIndex{four}\). Considering motility is relative, the spaceship would seem to be stationary and Earth would announced to motility. (This is the sensation you lot have when flight in a jet.) Looking out the window of the spaceship, the astronaut would see fourth dimension slow downwardly on Earth past a cistron of \(\gamma = xxx.0\). Seen from the spaceship, the earthbound sibling volition have anile only 2/thirty, or 0.07, of a year, whereas the astronaut would have aged 2.00 years.

Figure \(\PageIndex{4}\): The twin paradox consists of the alien conclusions near which twin ages more than as a effect of a long space journey at relativistic speed.

The paradox here is that the two twins cannot both be correct. As with all paradoxes, conflicting conclusions come up from a false premise. In fact, the astronaut's motion is significantly different from that of the earthbound twin. The astronaut accelerates to a loftier velocity and so decelerates to view the star system. To render to Earth, she again accelerates and decelerates. The spacecraft is not in a unmarried inertial frame to which the fourth dimension dilation formula tin be direct applied. That is, the astronaut twin changes inertial references. The earthbound twin does non experience these accelerations and remains in the same inertial frame. Thus, the situation is not symmetric, and it is incorrect to merits that the astronaut observes the aforementioned effects as her twin. The lack of symmetry between the twins will be still more axiomatic when nosotros analyze the journeying later in this chapter in terms of the path the astronaut follows through four-dimensional space-time.

In 1971, American physicists Joseph Hafele and Richard Keating verified time dilation at low relative velocities by flying extremely accurate atomic clocks around the globe on commercial aircraft. They measured elapsed time to an accuracy of a few nanoseconds and compared it with the time measured by clocks left behind. Hafele and Keating's results were within experimental uncertainties of the predictions of relativity. Both special and general relativity had to be taken into account, considering gravity and accelerations were involved as well as relative motion.

Practice \(\PageIndex{2A}\)

a. A particle travels at \(1.90 \times 10^8 \, m/s\) and lives \(2.ane \times 10^eight \, s\) when at rest relative to an observer. How long does the particle live every bit viewed in the laboratory?

Reply

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^two}}} = \dfrac{ii.10 \times 10^{-8}s}{\sqrt{1 - \dfrac{(i.90 \times ten^8 \, m/s)^2}{(3.00 \times 10^8 \, thousand/due south)^2}}} = 2.71 \times 10^{-8} \, southward. \nonumber\]

Exercise \(\PageIndex{2B}\)

Spacecraft A and B pass in opposite directions at a relative speed of \(4.00 \times x^7 \, chiliad/south\). An internal clock in spacecraft A causes it to emit a radio bespeak for 1.00 s. The calculator in spacecraft B corrects for the beginning and end of the bespeak having traveled different distances, to calculate the time interval during which send A was emitting the indicate. What is the time interval that the computer in spacecraft B calculates?

Answer

Merely the relative speed of the two spacecraft matters because in that location is no absolute motion through space. The betoken is emitted from a fixed location in the frame of reference of A, so the proper time interval of its emission is \(\tau = i.00 \, s\). The elapsing of the signal measured from frame of reference B is and then

\[\Delta t = \dfrac{\Delta \tau}{\sqrt{1 - \dfrac{v^2}{c^2}}} = \dfrac{one.00 \, s}{\sqrt{1 - \dfrac{(4.00 \times 10^7 \, m/s)^2}{(three.00 \times 10^8 \, m/s)^2}}} = 1.01 \, s. \nonumber\]

murphyperearged.blogspot.com

Source: https://phys.libretexts.org/Bookshelves/University_Physics/Book:_University_Physics_%28OpenStax%29/University_Physics_III_-_Optics_and_Modern_Physics_%28OpenStax%29/05:__Relativity/5.04:_Time_Dilation

Share this post